At this point, I’m officially four weeks into post-Segment exploration.
A number of friends have asked me what it’s felt like… whether I’ve felt bored or restless yet.
I do plan to get back to building products again (more on that soon), but I’d say the biggest change is that I feel a lot less ‘hurried’.
I don’t care about sleeping 9 hours per night. If a book takes me to a new concept, I don’t feel guilty about researching it for hours on end. I’ve been using some holiday coding puzzles as an excuse to learn Rust, with only a slight agenda towards building something serious with it. I’ve felt far more free to let my mind wander and develop a prepared mind for whatever’s next.
Writing
This week I wrote a post on advice for early stage startup founders. As you grow a company, it’s easy to forget about all the lessons that ‘got you there’. This post has advice for founders in the early days. It’s pulled from lessons I’ve observed after making a number of angel investments and watching everyone hit the same issues we did. Link
Interesting reading
ML: KompaRe: A knowledge Graph Comparative Reasoning System (via arXiv) — This paper is essentially trying to auto-detect fake news. In doing so, the team built a service which takes a look at various images and titles posted to different news stories and pieces of social media. They can then run machine learning to detect what’s going on in each image, add a knowledge graph (helicopter -> has range -> 550 miles), and then run constraint solving to detect when a news story may not be legit.
Systems: Pigasus (via Morning Paper) — a team managed to build a 100Gbps intrusion detection system on a single server!!! It is an absolutely wild amount of packets/flows for a single instance to process. The big ideas: offload more work to a custom FPGA rather than a CPU, and do the cheapest regex/matching up front to filter out the broadest number of packets right away. At Segment we had a few similar ideas of “optimize for the fast path” with centrifuge.
Systems: Virtual Consensus in Delos (via Daily Paper) — this presentation/paper is very applicable to folks at Segment. It comes from a team at Facebook, who had a similar ctlplane/dataplane architecture. They needed a new control plane storage system, that had the rich API of Mysql, but the fault tolerance of ZooKeeper. Where they ended up… something not crazy different from debezium/ctlstore! That said, they did a lot more in terms of iterating on the storage layer and adding a layer of “virtual consensus” where they could swap out different storage nodes. If you have 20m, I highly recommend watching the video.
Bio: Cognition all the way down (via HN) — if you enjoyed books like The Selfish Gene, you’ll probably enjoy this. The big idea is that individual proteins and cells can act as a sort of ‘prisoners dilemma’. By bonding together and sharing information, they will naturally achieve better outcomes. I don’t think I’d seen cells modeled in quite this way before… and yet.. it makes some sense!
Disease modeling
I’ve continued spending time on the MIT Computational Thinking course, mostly just as a fun way to blow off steam. It’s a potpourri of various science concepts, all taught in a scientific computing language called Julia.
The most recent section discusses how to model disease transmission. It’s given me a much more intuitive grasp of how a disease like COVID might spread!
The SIR Model
A pretty basic model that many epidemiologists use is what’s called the SIR model. This models individuals in a population as being…
Susceptible — at risk of being infected
Infected — currently infected, with some chance of infecting susceptible individuals, or recovering
Recovered — not at risk of infecting or being infected
Individuals move from S -> I -> R as they come in contact with other individuals. In the very basic model, we can set two variables:
p_infection — the probability that an infected individual will infect a susceptible individual
p_recovery — the probability that the infected individual will recover.
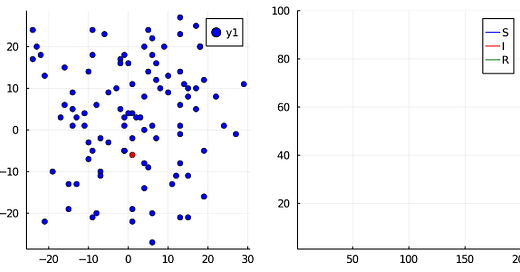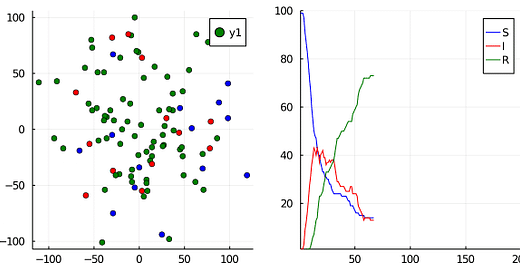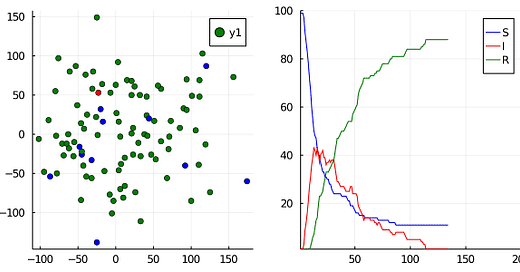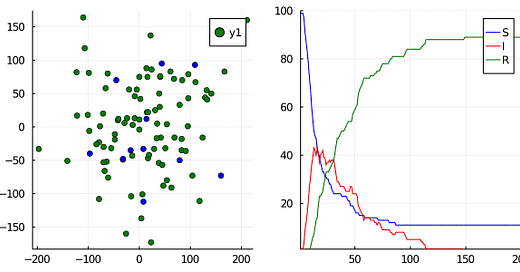
If we were to graph this, we can see individuals on the left infecting one another as they move via a random walk around a grid, and their total counts graphed on the right. (S = blue, I = red, R = green)
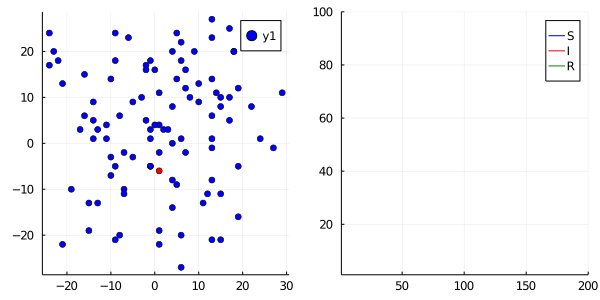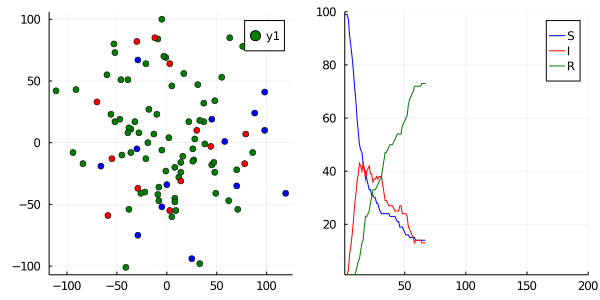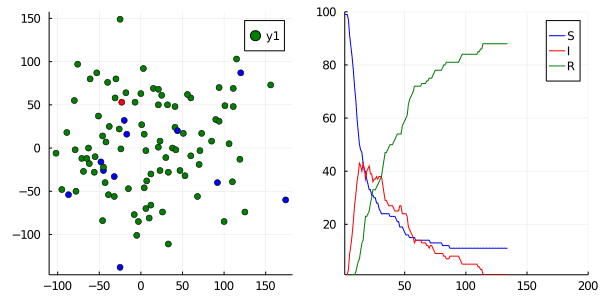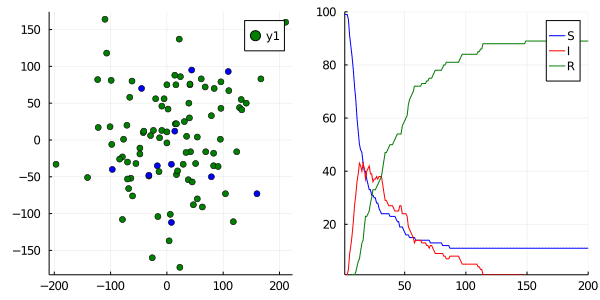
Comparing R0
If this model sounds basic, well, it is! But there’s a hidden benefit here. We can use Monte Carlo approximation and run this simulation hundreds of times to get a better sense of accuracy.
In doing so, we can start to get an estimation for the “R-value” or the transmission rate within our population. We can tweak our two parameters (p_infection, p_recovery) and compare this to real-world empirical data that we get from COVID-19 datasets. Pretty cool!
Here’s what my Julia code looks like to run a single interaction between two people

Stochastic models -> Differential Equations
Taking that one-step further, suppose we want to try and fit these parameters to real-world rates of covid that we’re seeing?
So far, we’ve used what we call a stochastic model. It’s generated by a random probability at each step. But really, we’d rather be able to express our model as a set of equations, that we can then solve for and minimize.
Enter Differential Equations… a subject that I literally have not revisited since college. We can effectively our counts for S, I, and R to the following three equations…
If this is straining your memories of calculus, bear with me, it did for me too.
Taking the first equation, we’re looking at the number of susceptible individuals at a time `t`, plus some delta `h`. It turns out that we can get this by taking the number of susceptible individuals at time `t`, and then subtracting the ones who were infected in the intervening time `h`. This is the second term: time infected (h) times beta (probability of infection) times number of susceptible individuals times number of infected individuals. We add it all up to get the value at s(t+h).
We then do the same thing for our other two equations, but using gamma as our probability of recovery.
Why differential equations? Gradient descent.
Well, if we have these functions as differential equations, we can do two things.
First, we can graph them and forecast as a set of lines and curves. Instead of needing to run this computationally intensive iterative process, we can just execute a few functions:
Second, we can optimize them! To do this, we can use a technique known as gradient descent. The general idea is that at each point, we look at the slope of our different parameters (in our case, p_infection and p_recovery) and determine how “far off” we are from minimizing the delta. [1]
Here, we can see that the parameters (3.9, -2) are the ones that minimize our differential equations.
Putting it all together: elementary Machine Learning
Okay, we have...
a discrete, stochastic model of our SIR graph
we've smoothed it out by running repeated trials and using monte carlo analysis
we've converted that graph into a set of differential equations which model the general phenomena we see
The last thing we have to do is figure out what the coefficients on that set of differential equations are. We can do this by applying a minimization function across our two variables we had earlier (p_infected and p_recovery). The computer effectively should do this for us.
And voila, we have our first "machine learning".
Next week: Raytracing.
Radical Markets
Roughly 3-4 times per year, I’ll find a book that is really surprising and novel. [2] Radical Markets is that book.
The core thesis of the book is that the debate around economic structures is incredibly limited. When we hear politicians and journalists talk, the proposals regularly fall into socialism vs capitalism.
When it comes to both socialism and capitalism, both doctrines ignore a big part of today’s problems: global inequality. Radical markets seeks to break outside those lines, and bring markets to new areas where they didn’t previously exist.
The book is structured as a series of 6 radical ideas. Each one starts with a vignette about how the future might look, before diving into specifics.
I’ll add one big caveat that I think these ideas are fascinating… but I struggle to see how we’d take steps towards getting them implemented. All of them are a big departure from the status quo, which is perhaps the point.
A (truly free) market for land
In some ways, land is the ultimate monopoly. Every parcel of land is completely unique, and the seller has complete ability to decide whether to sell their land or not.
The only entity who can force a sale of land is the federal government, using laws of eminent domain.
The result? Well, land doesn’t really rise to its most valuable usage. You see vacant lots and abandoned warehouses sitting in the heart of SF. Public works projects are blocked for years as developers try and negotiate the path for rail, airports, and the like. The results mean that society isn’t getting as much value from the land as we could.
The scheme outlined in the book takes a new approach, and here’s the idea…
anyone who owns land sets a public price on that land, which they’d update via an app
the owner pays taxes on that land at a certain percentage (say 7%) annually. there are no government appraisers, or other tax considerations
anyone can buy that land for the stated price at any time, and use it for whatever they’d like after a 3-month settling/move-out period. the owner can’t refuse
all of the taxes are redistributed as a ‘social dividend’, essentially a form of universal basic income.
The incentives are structured so that a land or homeowner won’t set too low of a price to avoid taxation, but also will set a price they are happy to receive and then move out. Any taxes paid via this scheme would be re-distributed per capita as a form of universal basic income, which helps reduce inequality.
A new model of voting
Historically, our democracy has worked via one-person, one-vote. It means that most choices are made via the majority.
But what about cases where a minority of people might care a lot about some issue, that is relatively insignificant to the majority?
In this case, the minority will typically always lose in an election, until a case is raised to the supreme court (see gay marriage), who notably is not elected by the majority, but appointed.
This new model of voting the authors introduce is known as “quadratic voting”. The rules behind it are interesting, though they can be hard to wrap one’s head around.
every election, each person gets the same number of “voice credits”
each voter can decide to turn the voice credits they have accrued into vote, or save those credits for a future election and issue
when an individual spends credits, the number of votes is equal to the square root of the number of credits used. (e.g. 4 credits means 2 votes, 9 credits means 3 votes, etc.)
The idea here is that as you try and add more votes to a given issue, the cost to do so gets more expensive. The goal is to allow a minority group to express views for an issue they care strongly about, while still balancing that against really fringe movements.
Even more radical, you could potentially imagine countries voting this way in international coalitions like the U.N. The authors propose a scheme where countries which exert more power get more credits. The idea is that it helps bring some sort of clear exchange to policies which right now happen through obfuscated negotiations.
I think this maybe the most achievable scheme to implement, not on a country level, but on a business level. You might imagine that if a corporate leadership team is trying to decide between different areas of a company strategy, they could each vote with some number of credits. They might even ask many different parts of the org to weigh in with their votes. Each subsequent vote from an individual gets more expensive to cast, which keeps people from pushing wholeheartedly for an idea unless they think it should really come at the cost of everything else.
Making visa sponsorship available to all
Since the push for free trade, we’ve seen markets expand drastically across the globe. More and more countries are able to freely trade goods and services.
And yet there’s a big piece that’s missing from that equation: labor! Most countries will happily accept new goods into their borders, but will put up large restrictions for accepting the workers who produce those goods.
In today’s economy, companies hold most of the power to sponsor new workers. Tech companies in particular are fond of using H1-B visas to continue to hire the best talent from all over the world.
And yet, that option isn’t available to most normal people. The authors present a new idea which would effectively open up individuals to sponsor immigrants.
there would be a significant fee that the immigrant would have to pay. even if this were thousands of dollars, the authors claim the earning differential of the US would outpace the cost.
the sponsor would be responsible for vetting and ensuring the immigrant could find work
the sponsor would receive a portion of the immigrant’s pay
I’m a bit more skeptical of this scheme, though generally speaking I’m a believer in opening up more immigration and more open borders.
Breaking up institutional investors
There’s this infamous “rule of institutional investors” that Matt Levine talks a lot about. The general idea is that most of the world’s public companies are owned by a small number of very large asset managers: Blackrock, Vanguard, Fidelity, and friends (e.g. Vanguard is the largest holder of TWLO, followed by Morgan Stanley).
These institutional investors tend to be more in the business of owning these assets on behalf of pension funds, retirement accounts, and endowments. Yet there’s some evidence that there’s a more pernicious aspect to them owning ~20-30% of most large cap public companies.
The authors make the claim that this shared ownership causes companies to be less competitive. The general idea is that in a monopoly, prices are exorbitant, because there is no substitute. In duopoly, prices are less than a monopoly, but higher than if there are three competitors, etc, etc.
Therefore, it is in the interest of the institutional investors for their companies not to be too competitive. After all, if you are an investor who owns 30% of United, 30% of Delta, and 30% of Southwest… you might think about nudging each of their CFOs to avoid undercutting the competition on price.
The result is a system which isn’t exactly governed by the rules of U.S. anti-trust law, but also isn’t as competitive as it could be. The authors propose a scheme where…
an institutional investor could own as much of they like of one company in a given industry (e.g. you could own United or Delta, but not both)
an institutional investor could not hold more than 1% of two companies which compete
There’s a lot of details to sort out with this one, but the gist is that having a more concentrated interest within a single industry, while maintaining a diversified position across industries still gives you diversified returns, while increasing competition.
Paid for your data
Today, the biggest companies in the world are more or less powered by data. Facebook, Google, Amazon, Netflix-all of them profit wildly off their ability to understand and market to their users.
The author’s argue that there’s something a bit unequal about this outcome… that even though Facebook is providing a great service to you for free, they tend to make far more money than each user would be willing to pay. The result is a scheme where…
each user would get paid a certain amount for submitting information that the company can use
because information becomes a paid service, tech companies could stop taking shady actions to try and capture data and just be up-front about what data they need, and pay for it
individual creators can make a livable wage by supplying valuable data
In effect, the scheme mirrors exactly what Nielsen used to do in the age of TV by paying people to respond to surveys about what they watch, or what Mechanical Turk aims to do now.
I’ll say that I’m pretty dubious of this proposal, both in terms of the incentives and the implementation. I don’t think large tech companies have much incentive to adopt this pattern, as it puts more of a focus on an area that both they and most users seem somewhat content to ignore this idea vs pay for a service. Perhaps we’ll see more paid services arise in the future.
Capitalism as a computer
One last final thought that I thought was interesting-modeling capitalism and free markets as a way of detecting information.
Effectively most markets move based upon a single set of inputs: the price of goods. The U.S. government doesn’t need to figure out how much corn should be produced by each individual farmer, each farmer can make their own choice depending on the price they can buy, cultivate, and sell corn crops at.
In this way, we’ve thought of free markets as having the best exchange of information for the last hundred years. No centrally planned system could even come close to understanding all of our innate preferences, or even the supply chains for fulfilling millions of different types of goods each day. Instead, each individual closest to a domain sets the prices, and then acts on those decisions.
But it does make you wonder… could there ever be such a system? Could there eventually be a computer system powerful enough to ensure that food always made it to those who need it?
This idea sounds farfetched to me, in part because of how bad computers are at understanding and modeling human preferences outside of the market context. Outside of a service knowing who our friends are, or what shows I want to watch next… how much more advanced would a system have to be to understand my hopes and dreams? It certainly seems like an area of HCI which is underexplored.
[1] Incidentally, this is exactly how machine learning works when we apply training to neural nets.
[2] I’ve really been trying to find a way to up this number, but it seems incredibly dependent on “surprise”, whether the information in a book is really new to me. If you have recommendations, please send them my way.